Fuqi Jia
LLM-Guided Quantified SMT Solving over Uninterpreted Functions
Jan 08, 2026Abstract:Quantified formulas with Uninterpreted Functions (UFs) over non-linear real arithmetic pose fundamental challenges for Satisfiability Modulo Theories (SMT) solving. Traditional quantifier instantiation methods struggle because they lack semantic understanding of UF constraints, forcing them to search through unbounded solution spaces with limited guidance. We present AquaForte, a framework that leverages Large Language Models to provide semantic guidance for UF instantiation by generating instantiated candidates for function definitions that satisfy the constraints, thereby significantly reducing the search space and complexity for solvers. Our approach preprocesses formulas through constraint separation, uses structured prompts to extract mathematical reasoning from LLMs, and integrates the results with traditional SMT algorithms through adaptive instantiation. AquaForte maintains soundness through systematic validation: LLM-guided instantiations yielding SAT solve the original problem, while UNSAT results generate exclusion clauses for iterative refinement. Completeness is preserved by fallback to traditional solvers augmented with learned constraints. Experimental evaluation on SMT-COMP benchmarks demonstrates that AquaForte solves numerous instances where state-of-the-art solvers like Z3 and CVC5 timeout, with particular effectiveness on satisfiable formulas. Our work shows that LLMs can provide valuable mathematical intuition for symbolic reasoning, establishing a new paradigm for SMT constraint solving.
Can Graph Neural Networks Learn to Solve MaxSAT Problem?
Nov 15, 2021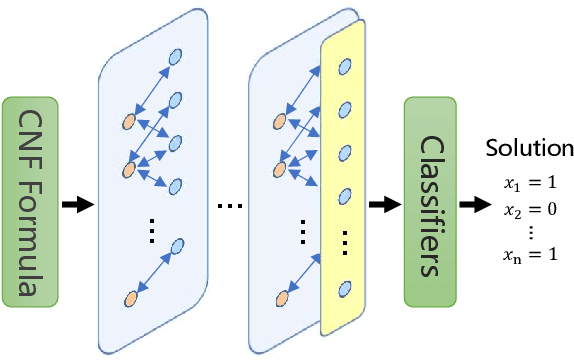
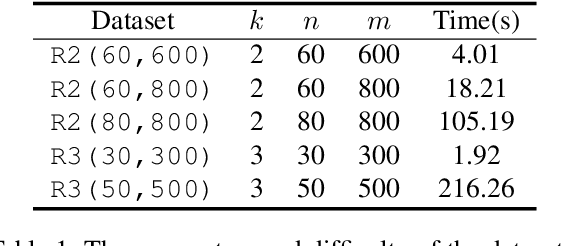
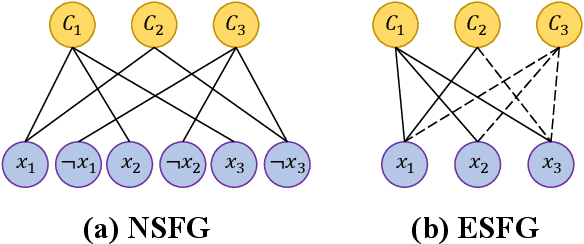

Abstract:With the rapid development of deep learning techniques, various recent work has tried to apply graph neural networks (GNNs) to solve NP-hard problems such as Boolean Satisfiability (SAT), which shows the potential in bridging the gap between machine learning and symbolic reasoning. However, the quality of solutions predicted by GNNs has not been well investigated in the literature. In this paper, we study the capability of GNNs in learning to solve Maximum Satisfiability (MaxSAT) problem, both from theoretical and practical perspectives. We build two kinds of GNN models to learn the solution of MaxSAT instances from benchmarks, and show that GNNs have attractive potential to solve MaxSAT problem through experimental evaluation. We also present a theoretical explanation of the effect that GNNs can learn to solve MaxSAT problem to some extent for the first time, based on the algorithmic alignment theory.
ε-weakened Robustness of Deep Neural Networks
Oct 29, 2021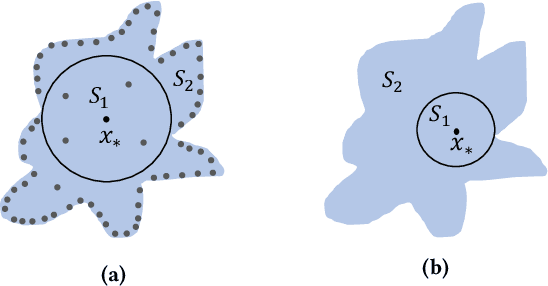

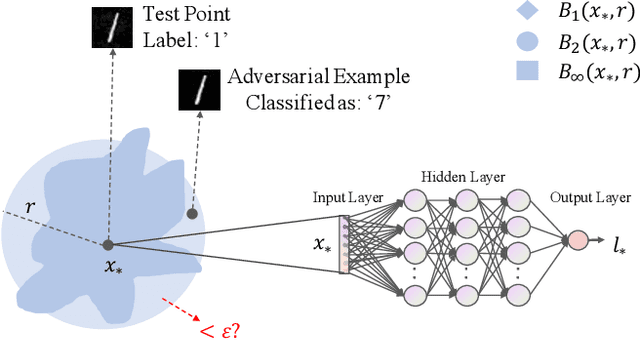
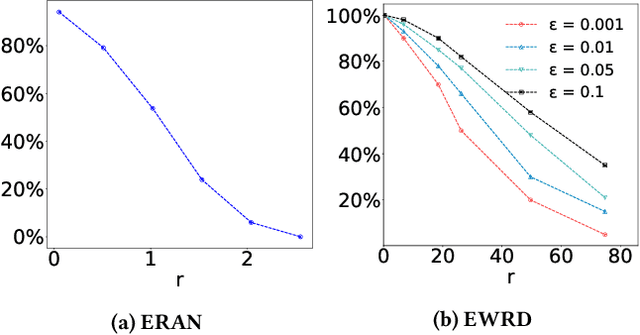
Abstract:This paper introduces a notation of $\varepsilon$-weakened robustness for analyzing the reliability and stability of deep neural networks (DNNs). Unlike the conventional robustness, which focuses on the "perfect" safe region in the absence of adversarial examples, $\varepsilon$-weakened robustness focuses on the region where the proportion of adversarial examples is bounded by user-specified $\varepsilon$. Smaller $\varepsilon$ means a smaller chance of failure. Under such robustness definition, we can give conclusive results for the regions where conventional robustness ignores. We prove that the $\varepsilon$-weakened robustness decision problem is PP-complete and give a statistical decision algorithm with user-controllable error bound. Furthermore, we derive an algorithm to find the maximum $\varepsilon$-weakened robustness radius. The time complexity of our algorithms is polynomial in the dimension and size of the network. So, they are scalable to large real-world networks. Besides, We also show its potential application in analyzing quality issues.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge